Un peu d’histoire
La “méthode historique” fut inventée par le mathématicien britannique Charles Babbage, connu notamment pour ses machines à différence, vers 1854 mais sa découverte resta ignorée en l’absence d’écrit. Pendant ce temps, un officier prussien à la retraite, Friedrich Kasiski, parvint au même résultat et publia en 1863 “Die Geheimschriften und die Dechiffrir-Kunst”.

Charles Babbage
Pour déchiffrer un tel code, la première étape est de déterminer la longueur du mot-clef. Avec un chiffre de Vigenère, si une même séquence de lettres dans le texte en clair a été cryptée avec une même partie de mot-clef, elle donnera alors une même séquence de lettres cryptées. Si une séquence de lettres en clair est fréquente dans le texte alors la probabilité qu’elle soit codée avec une même partie du mot-clef sera plus forte, ce qui permet de détecter sa présence en recherchant des séquences de lettres identiques dans le texte chiffré. Pour faire cette détection de façon statistiquement fiable, une séquence d’au moins trois lettres est préférable et doit se répéter plusieurs fois dans le texte. De telles séquences varient suivant le type de texte, mais par exemple, en français, la séquence « LES » peut se retrouver assez souvent dans la plupart des textes.
Babbage et Kasiski se sont donc tous deux appuyés sur la répétition d’une séquence de 3 lettres dans le message chiffré et ont calculé la distance entre elles dans le message, ce qui revient à calculer par combien de lettres elles sont séparées l’une de l’autre. En calculant le Plus Grand Commun Diviseur (PGCD) des distances on obtient la longueur probable de la clef. En pratique, étant donné un message chiffré comportant deux séquences répétées S et T, on note l’emplacement dans le message de leurs répétitions S1, S2, T1 et T2. La longueur probable de la clef est :
\[PGCD (S2-S1 ; T2-T1)\]Il faut ensuite déterminer le mot-clef grâce à l’analyse des fréquences et déchiffrer le texte avec le mot-clef.
Un outil mathématique : l’indice de coïncidence
En 1920, le cryptologue de l’armée américaine Willian Friedman met au point l’indice de coïncidence. Avec un texte de n lettres et \(n_{i}\) occurences d’une lettre donnée dans le message, on a :
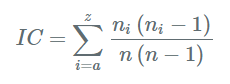
En supposant que la clef est d’une longueur k, on regarde une lettre sur k et on calcule l’indice de coïncidence pour cette série de lettres. En effet, prendre une lettre sur k revient à prendre une série de lettres toujours chiffrée avec le même décalage, l’indice de coïncidence est donc égal à celui du texte clair. Quand on cherche la longueur k de la clef pour la cryptanalyse d’un texte, k est très probablement la valeur testée pour laquelle l’indice de coïncidence est particulièrement élevé.
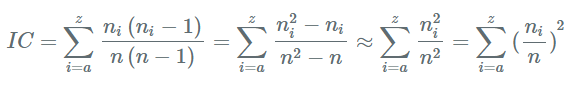
Ici \(n\) est la longueur du message et \(n_{i}\) est la fréquence d’apparition de la lettre i dans le texte.
Dans sa définition de l’indice de coïncidence, Friedman utilise, à la place du carré traditionnel, le carré utilisé en statistiques défini par \(x \times (x-1)\) qui offre de meilleures propriétés dans le problème donné. Le calcul ci-dessus montre que si la taille du message est suffisamment grande, alors l’indice de coïncidence se rapproche de la somme des écarts types des fréquences d’apparition des lettres. C’est pour cela qu’en pratique et notamment en informatique on utilise plus souvent cette seconde énonciation.
…mais aussi informatique !
Indice de coïncidence du texte en fonction de la taille de la clef utilisée pour le chiffrer
Comme illustration d’un exemple de cryptanalyse, nous avons réalisé une expérience d’analyse à la main d’un message chiffré avec le chiffre de Vigenère. Nous avons pour ce faire utilisé la méthode de Babbage et Kasiski. Cliquez ici pour accéder au compte-rendu de notre expérience.