Eléments de contexte
Le problème de distribution de la clef a été le problème constant des cryptographes au cours de l’histoire. Pendant la seconde guerre mondiale, le haut commandement allemand devait ainsi distribuer le registre mensuel des clefs quotidiennes à tous les opérateurs d’Enigma, ce qui constituait un problème de logistique considérable.
La distribution des clefs constitua le problème primordial pour les cryptographes de l’après-guerre. La cryptologie était vouée à se développer pour des applications civiles et quotidienne, telles que le commerce, l’échange d’e-mail, etc. via internet. Il fallait pour cela qu’elle soit capable d’assurer son objectif premier, c’est-à-dire protéger la confidentialité des données. Pour les transactions commerciales, le dilemme se posait clairement : si les gouvernement, avec tout leur argent, avaient peine à garantir la sécurité de leurs clefs, comment des entreprises civiles pourraient-elles jamais espérer jouir d’une distribution de clefs sûre et non ruineuse ?
Ce problème ne fut résolu que durant les années 70.
Avec l’ère d’Internet, les mathématiciens s’intéressent particulièrement à la cryptograhie.
Ce sont deux américains, Whitfield Diffie et Martin Hellman de l’Université de Stanford qui en 1976, créent une nouvelle forme de cryptographie, dite asymétrique ou à clef publique. Ils recevront par la suite nombre de prix pour cette découverte.

Whitfield Diffie (à gauche) et Martin Hellman (à droite)
Ils s’appuient pour leur protocole sur l’arithmétique modulaire, très utilisée en cryptographie moderne.
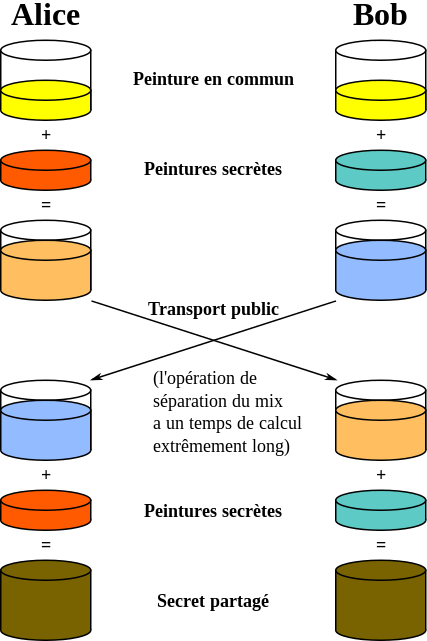
Une analogie avec de la peinture pour comprendre
Modélisation mathématique et fonctionnement
- Alice et Bob veulent s’échanger une clef
- Alice choisit un grand nombre premier \(p\) et une base \(g\) avec \(g \leq p\)
- Elle choisit un nombre secret a
- Elle envoie à Bob le nombre \(A = g^a \bmod p\)
- Bob choisit à son tour le nombre secret b
- Il envoie à Alice \(B = g^b \bmod p\)
- Alice peut déterminer la clef secrète : \(B^a \bmod p = (g^b)^a \bmod p = = g^{ba} \bmod p = g^{ab} \bmod p\)
- Bob en fait de même et obtient la clef identique : \(A^b \bmod p = (g^a)^b = g^{ab} \bmod p\)
Ceci est rendu possible par la commutativité de la fonction puissance !
En connaissant p, g, A et B, il faudrait en revanche effectuer des calculs fort complexes pour trouver la clef secrète \(g^{ab}\)
Exemple (on considérera des petits entiers par souci de simplicité)
- Alice et Bob définissent p = 41 et g = 6
- Alice choisit comme nombre secret a = 7
- Elle envoie à Bob le nombre \(6^7 \bmod 41 = 29\)
- Bob choisit à son tour le nombre secret 15
- Il envoie à Alice \(6^{15} \bmod 41 = 3\)
- Alice peut déterminer la clef secrète : \(3^7 \bmod 41 = 14\)
- Bob en fait de même et obtient la clef identique : \(29^{15} \bmod 41 = 14\)
Alice et Bob ont bien partagé la clef 14 !