Principe général
La machine Enigma était faite de composants ingénieux combinés dans une incroyable machine à chiffrer. Toutefois, si on les prend un à un, ses principes de base deviennent compréhensibles. Enigma est la première méthode de cryptographie électronique.

Machine Enigma avec ses parties légendées
Dans sa forme élémentaire, Enigma consiste en trois éléments reliés par des câbles : un clavier pour entrer chaque lettre du texte clair, un brouilleur qui crypte chaque lettre du texte clair en une lettre chiffrée, et un tableau lumineux fait d’un certain nombre de lampes pour afficher la lettre du texte crypté. Pour crypter une lettre du texte clair, on envoie une impulsion électrique qui passe dans le brouilleur puis allume une lampe du tableau, qui indique la lettre correspondante du texte chiffré. On y ajoutera par la suite le tableaux de connexions pour augmenter le nombres de possibilités
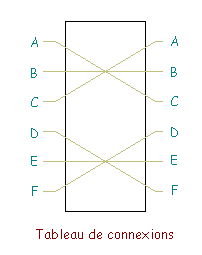
Le tableau de connexions
Dans ce tableau, chaque entrée de fil correspond à une lettre. Les utilisateurs possèdent 6 fils qui permettent d’appareiller les lettres deux à deux. En reliant deux lettres entre elles avec ces fils, on les échange. Dans le schéma d’exemple ci-dessous, le A est relié au C et le D est relié au F. Ainsi, lorsqu’on tapera la lettre A sur le clavier, le signal sera détourné à C avant d’entrer dans le brouilleur. Cela semble assez simple mais c’est en réalité le tableau de connexions qui rend le nombre de clefs potentielles énorme (voir calcul ci-dessous).
Le brouilleur
La partie centrale de la machine, le brouilleur, est un tambour en matériau isolant portant sur chaque face des contacts électrique. Chaque lettre du clavier est reliée à une entrée de ce tambour. Venant du clavier, les fils pénètrent dans le tambour en 26 points, font à l’intérieur un parcours animé de boucles et de virages, et ressortent sur l’autre face en 26 autres points. Ces 26 autres points allument sur le tableau lumineux la lettre cryptée. Les montages internes déterminent ainsi comment les lettres du texte clair seront cryptées. Ce brouilleur peut se diviser en deux parties.
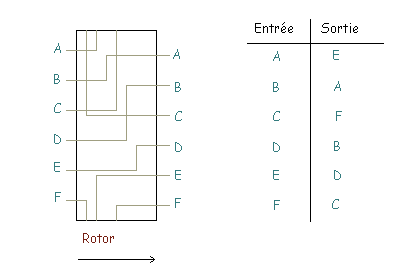
Les rotors
Ils sont passés de 3 à 6 au cours de la guerre. A chaque lettre entrée correspond une autre lettre. De plus, à chaque lettre frappée, un ou plusieurs des rotors mobiles tourne, changeant la substitution qui sera opérée à la prochaine touche pressée.
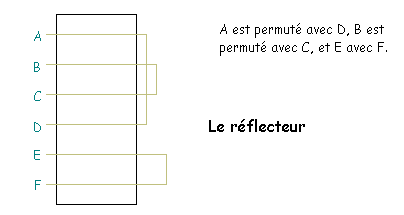
Le réflecteur
Au bout des 3 rotors se situe une dernière permutation qui permet de revenir en arrière. On permute une dernière fois les lettres 2 par 2, et on les fait retraverser les rotors, et le tableau de connexion.
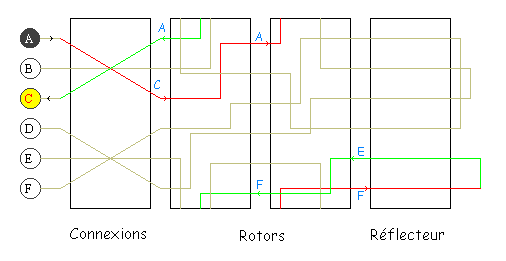
Dans le schéma simplifié (2 rotors, 6 lettres) ci-dessous, la lettre A sera codée C. En partant de A :
- on traverse le tableau de connexions : on obtient C.
- on traverse les 2 rotors : on obtient successivement A et F.
- on traverse le réflecteur où on obtient E, puis on renvoie dans les rotors pour obtenir F, A et finalement C après le tableau de connexions.
Remarques :
-
Si on avait tapé C, le courant aurait circulé dans l’autre sens et on aurait obtenu A. C’est le réflecteur qui garantit le caractère involutif de l’Enigma : chiffrer est identique à déchiffrer, ce qui en fait un chiffrement symétrique.
-
Le réflecteur empêche Enigma de substituer une lettre à elle-même dans le texte chiffré ; la lettre A ne sera jamais chiffré A. C’est une faille majeure qui a été utilisée par les cryptanalystes.
Utilisation d’Enigma par l’armée allemande
Les opérateurs allemands recevaient chaque mois un carnet de code contenant toutes les clefs quotidiennes du mois. La clef du jour comprenait :
- le choix et l’ordre des trois rotors
- la position initiale de chacun de des rotors
- les associations du tableau de connexions
Une fois ces installations faites chez l’émetteur et le récepteur, le premier chiffreur choisit au hasard 3 lettres qui seront le véritable réglage de rotors et les frappe deux fois, ex : SHMSHM. C’est la clef brute du message. Il envoie ces 6 lettres au récepteur, les deux opérateurs sont ainsi au courant de la véritable clef du message. Ils règlent tous deux, à nouveau, leur rotors en fonction de cette clef. Le message peut maintenant être envoyé.
Pour ce faire, l’émetteur frappe sur le clavier le message qu’il veut coder. A chaque lettre tapée, une lettre s’allume sur l’écran au-dessus du clavier et indique le résultat du codage. Il note alors cette lettre puis la transmet par radio, en morse, au récepteur.
Calcul du nombre de clefs potentielles avec 3 rotors :
- Orientation des brouilleurs
- Chacun des rotors peut être réglé sur 1 des 26 positions. Il y a donc \(26 \times 26 \times 26 = 17 576\) dispositions
- Disposition des brouilleurs
- Les trois rotors (ici nommés A, B, C) peuvent être placés selon les 6 dispositions suivantes : ABC, ACB, BCA, BAC, CAB, CBA ce qui fait \(3! = 6\) dispositions
- Tableaux de connexions
- Le nombre de branchements possibles en appairant 6 fois 2 lettres prises parmi les 26 lettres de l’alphabet est énorme.
- D’abord il faut choisir 12 lettres parmi 26 : pour la première lettre, on a 26 possibilités mais pour la deuxième lettre plus que 25, puis pour la troisième lettre 24, pour la quatrième 23, … et pour la douzième, 15 possibilités. Cela fait \(26 \times 25 \times 24 \times 23 \times 22 \times 21 \times 20 \times 19 \times 18 \times 17 \times 16 \times 15 = 4, 626053752 \times 10^{15}\) possibilités. Cependant, comme l’ordre des 12 lettres n’a pas d’importance, il faut diviser ce nombre par 12! ce qui fait \(9,6577 \times 10^{6}.\)
- Maintenant, il faut choisir 6 paires de lettres parmi 12, soit \(12!/6! = 6,6528 \times 10^{5} \times
9,6577 \times 10^{6} \times 6,6528 \times 10^{5} = 6, 425074656 \times 10^{12}\)
Enfin, comme la paire (A,B) donne la même connexion que (B,A), il faut diviser par 2 pour chaque fils c’est à dire par 26 :
\(6, 425074656 \times 10^{12} / 26 = 100 391 791 500\)
On peut résumer ces calculs avec le calcul suivant :
\(\frac{26!}{14! \times 6! \times 26} = 1, 003917915 \times 10^{11}\)
Le nombre total de clefs est égal au produit de ces trois facteurs \(17 576 \times 6 \times 100 391 791 500 = 1,058691676 \times 10^{16}\) ce qui est environ égal à \(10^{16}\) possibilités, ce qui est énorme pour l’époque.