Exemple d’une cryptanalyse : notre compte-rendu d’expérience
Dans l’esprit des TPE de 1ère S, nous nous sommes confrontés à une expérience de cryptanalyse. Nous rendons compte ici de notre démarche de recherche pour résoudre ce problème.
Nous cherchons à décrypter le texte suivant :
ATKUTESAATQNJAXANBWPQTBWYEHKCVQSVZSBIIMWEUYXIZDKHZATXMGAUXAPMIYAILNUCWEABWYDEXTIERGXMPEYLIXIIMWPEYXPGSHMEGXJMRASPWYDSGAWQZJMQMLNMYDEAFMOIHIWHOAAMYPRWVQNZKSGLKHGAURMDBOAZIGXVZIZEFIZQCRMYDSPWYDSRMWEOOVWCUOTIEDKDSDETBSGBRQILLKALQUXMYJMGQWVEJMQMNJMIZVGQRCUKTUGEYUSYETBWQNIWVQLKBIYPYUIOHGXTQEZNYUTPMHUSGKIFTKVYUTYWMEPRCWXETBIQTRIYDOXMZMDOAWUPKZPMNAQX
Nous supposons dans notre raisonnement que le texte codé est en français.
1. Hypothèse “Chiffre de César”
-
Hypothèse : Nous supposons que le texte est codé avec un chiffrement de substitution mono-alphabétique (une lettre est toujours codée par une même autre lettre) et plus précisément un chiffre de César, c’est-à-dire un décalage alphabétique de quelques crans (jusqu’à 26) vers la droite ou vers la gauche.
-
Si c’est un chiffre de César, alors les fréquences d’apparition de chaque lettre devraient être similaires à celle d’un texte français : avec d’importantes variations comme par exemple une fréquence élevée pour la lettre “e” et beaucoup plus faible pour le “k” ou le “w”. Nous allons donc compter le nombre d’apparitions de chaque lettre et en déduire leur fréquence que nous comparerons ensuite aux fréquences moyennes trouvées dans la langue française.
-
Résultats : Nous voyons que les fréquences mesurées sont moins dispersées par rapport à la langue française (voir figure 1). Ainsi, aucune lettre ne se distingue clairement: la lettre la plus fréquente est à 7,2 % (pour la lettre M) contre 15,9 % pour le E en français.
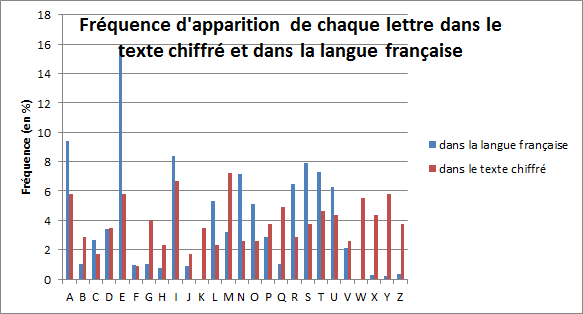
Figure 1
Le graphique montrant la corrélation entre la fréquence mesurée et celle de la langue française est donné en figure 2. Nous voyons que les points y sont très dispersés, indiquant une faible corrélation entre les deux.
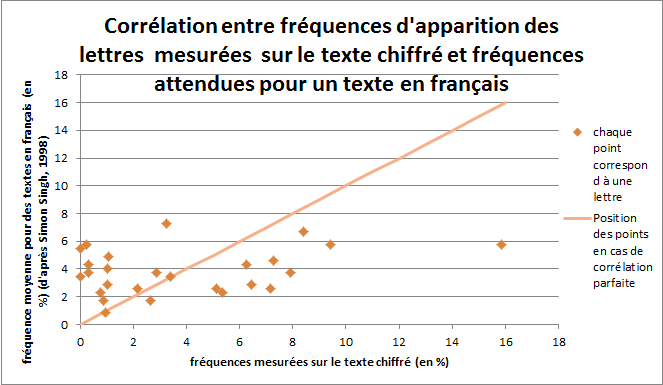
Figure 2
-
Les résultats précédents nous montrent que la fréquence d’apparition des lettres du texte chiffré ne correspond pas à celle d’un texte en français dont une lettre aurait été chiffrée toujours par une même autre.
-
Nous pouvons en conclure que ce texte n’est pas chiffré selon une méthode de chiffrement par substitution mono-alphabétique. Notre hypothèse 1 est fausse.
2. Hypothèse “Chiffre de Vigenère”
- Hypothèse : nous supposons que le texte est codé avec le chiffre de Vigenère. C’est un chiffrement par substitution polyalphabétique utilisant 26 alphabets codés distincts et un mot-clef pour chiffrer ou déchiffrer un message. Chaque lettre du mot-clef détermine un alphabet de substitution.
Il existe deux grandes méthodes de déchiffrement :
- Méthode moderne : l’indice de coïncidence. Le test de l’indice de coïncidence consiste à prendre une lettre sur n dans le message, et de mesurer l’indice de coïncidence. Cela nécessite de calculer l’indice de coïncidence pour le texte en prenant toutes les lettres (comme fait précédemment) puis une lettre sur 2, puis en ne prenant qu’une lettre sur 3, etc… On calcule l’indice de coïncidence à chaque fois. L’indice de coïncidence maximal est obtenu quand le texte est le moins aléatoire possible.
Nous avons tenté de calculer l’indice de coïncidence pour une clé de longueur 2 ; au vu du temps que cela nous a pris, nous en avons conclu que cette méthode était inapropriée pour trois lycéens armés seulement de stylos et de feuilles.
-
Méthode historique : Dans la seconde moitié du XIXe siècle, le mathématicien anglais Babbage et l’officien prussien Kasiki parvinrent quasiment en même temps à briser le chiffre de Vigenère. Pour déchiffrer un tel code, la première étape est de déterminer la longueur du mot clé, puis de déterminer le mot-clé lui-même. On commence par chercher des séquences d’au moins trois lettres qui apparaissent plus d’une fois dans le texte. Nous calculerons ensuite l’espacement entre elles afin de trouver la longueur du mot-clé. Puis nous déterminerons le mot-clé grâce à l’analyse des fréquences.
-
Recherche de la longueur du mot-clé: Nous relevons plusieurs séquences qui se répètent, elles sont en couleur dans le texte ci-dessous.
ATKUTESAATQNJAXANBWPQTBWYEHKCVQSVZSBIIMWEUYXIZDKHZATXMGAUXAPMIYAILNUCWEABWYDEXTIERGXMPEYLIXIIMWPEYXPGSHMEGXJMRASPWYDSGAWQZJMQMLNMYDEAFMOIHIWHOAAMYPRWVQNZKSGLKHGAURMDBOAZIGXVZIZEFIZQCRMYDSPWYDSRMWEOOVWCUOTIEDKDSDETBSGBRQILLKALQUXMYJMGQWVEJMQMNJMIZVGQRCUKTUGEYUSYETBWQNIWVQLKBIYPYUIOHGXTQEZNYUTPMHUSGKIFTKVYUTYWMEPRCWXETBIQTRIYDOXMZMDOAWUPKZPMNAQX
Pour trouver la longueur du mot-clé, on analyse l’espacement en nombre de lettres entre les occurrences de chaque séquence. Comme illustré dans l’exemple ci-dessous on voit que l’espacement entre les occurrences d’une séquence (ici “DPP” correspondant au mot “thé”) correspond à la longueur du mot clé (ici 4) ou à un multiple de cette longueur (8, 12, 16, etc)
| Mot-clé | KILOKILOKILO |
| Texte clair | théathébthéc |
| Texte chiffré | DPPODPPPDPPQ |
| Position | 1---5---9--- |
Le tableau 1 donne les résultats de notre analyse. Il apparaît clairement que toutes les périodes sont divisibles par 5. La première séquence SPWYDS peut résulter d’un mot-clé qui tourne 15 fois entre sa première et sa deuxième occurrence. La deuxième séquence BMY peut résulter d’un mot-clé qui tourne 10 fois entre ses deux occurrences,etc. Le mot-clé est donc sûrement composé de 5 lettres. Une autre méthode possible consiste à calculer le PGCD des écarts. PGCD (75 ; 50 ; 105; 115 ; 15) = 5.
| Séquence répétée | Espace de répétition | Longueurs de clefs possibles | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 5 | 7 | 10 | 15 | 21 | 23 | 25 | 35 | 50 | 75 | ||
| SPWYDS | 75 | x | x | x | x | x | |||||||
| BWY | 50 | x | x | x | x | x | |||||||
| GAU | 105 | x | x | x | x | x | x | ||||||
| JMQM | 115 | x | x | ||||||||||
| YUT | 15 | x | x | x | |||||||||
Table 1
- Il s’agit désormais de découvrir les lettres du mot-clé en question. Appelons le mot-clé L1-L2-L3-L4-L5 représentant la première lettre du mot-clé et ainsi de suite. La lettre L1 définit une ligne du carré de Vigenère, et procure un alphabet chiffré de substitution monoalphabétique pour la première lettre du texte en clair. Toutefois, pour crypter la deuxième lettre du texte clair, le cryptographe aura utilisé L2 pour définir une autre ligne du carré de Vigenère, procurant évidemment un autre alphabet chiffré de substitution monoalphabétique. La troisième lettre serait cryptée suivant L3, la quatrième suivant L4 et la cinquième suivant L5. Chaque lettre du mot-clé fournit un alphabet chiffré différent. Toutefois, la sixième lettre du texte clair sera à nouveau cryptée selon L1, la septième lettre selon L2 et le cycle se répète jusqu’au bout. En d’autres termes, le chiffre polyalphabétique est fait de 5 chiffres monoalphabétique, chaque chiffre monoalphabétique est responsable d’un cinquième du message. Or nous savons comment analyser des chiffres monoalphabétiques.
Nous savons que l’une des lignes du carré de Vigenère, définie par L1, commande l’alphabet chiffré pour la 1ère, la 6e, la 11e, la 16e… lettre du message. Donc si nous regardons la 1ère, la 6e, la 11e, la 16e… lettre du texte chiffré, nous pourrons utiliser l’analyse des fréquences pour déterminer l’alphabet en question. Nous calculons donc la fréquence de chaque lettre mais uniquement en en prenant une sur cinq.
La figure 3 ci-dessous montre la fréquence de distribution des lettres apparaissent à la 1ère, la 6e, la 11e, la 16e… places dans le texte chiffré, soit A, E, Q, A … Maintenant, rappelons-nous que chaque alphabet chiffré du carré de Vigenère est un simple alphabet normal, décalé de un à vingt-six crans. Par conséquent, la répétition ci-dessus devrait présenter des traits communs avec celle d’un alphabet normal, bien que décalée d’une distance indéterminée. En comparant la répartition L1 à la répartition banale, on devrait pouvoir repérer le décalage. La figure 4 illustre la répartition habituelle des lettres en français.
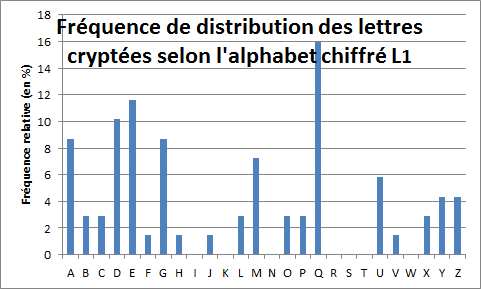
Figure 3
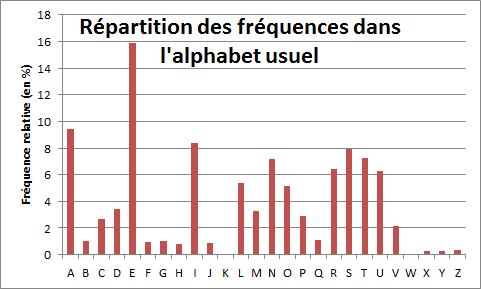
Figure 4
Le graphique de la répétition usuelle est animé de pics, de plateaux et de creux. Son pic le plus important se trouve sous le E, précédé d’un creux sous BCD avec, pour A une présence relativement importante. Nous retrouvons dans la répartition de fréquences L1 un schéma du même type avec un pic pour Q, un creux pour NOP et un M un peu plus long. Cela nous donne envie de superposer les alphabets en faisant coÏncider le Q de l’alphabet chiffré avec le E de l’alphabet normal. Dans le cas où les deux graphiques présenteraient alors à peu près la même silhouette, nous pourrions en déduire que la première lettre du mot-clé, L1, est probablement M.
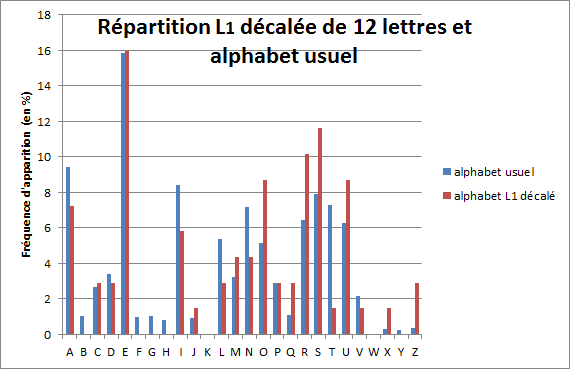
Figure 5
Cette superposition confirme la ressemblance entre les graphiques, nous montrant ainsi que la séquence X-Y-Z-A-B-C-D semble se présenter comme L-M-N-O-P-Q-R dans l’alphabet usuel, ce qui confirme que L1 est M. On peut également le vérifier en étudiant la corrélation entre l’alphabet L1 décalé de douze lettres et la fréquence moyenne sur un texte français.
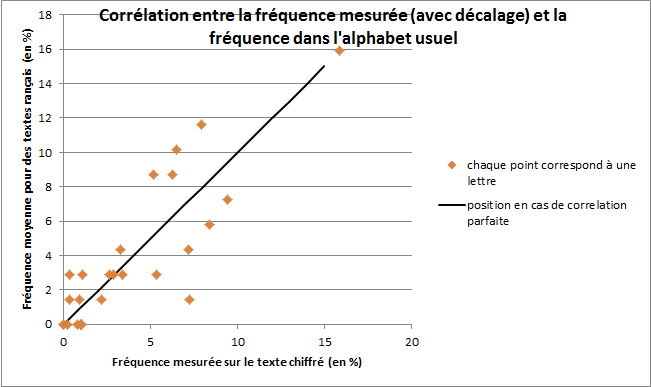
Figure 6
La corrélation est correcte et nous permet de confirmer notre hypothèse. Elle n’est pas parfaite car l’analyse des fréquences est réalisée sur un texte de 69 lettres, ce qui est relativement peu. Pour avoir une corrélation quasi-parfaite, il faudrait un échantillon d’environ 10 000 caractères.
Nous allons recommencer la même démarche pour identifier la deuxième lettre du mot-clé. Une répartition des fréquences une fois établie pour la 2e, la 7e, la 12e, la 17e … lettres du texte chiffré, nous comparons de nouveau le graphique obtenu avec celui de l’alphabet courant (figure 7).
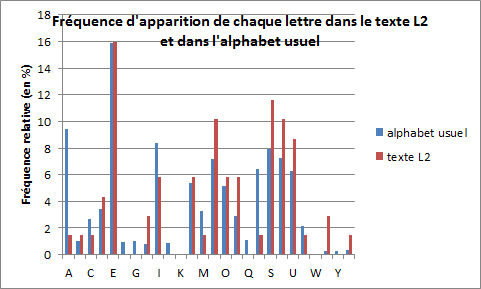
Figure 7
Les fréquences de L2 semble correspondre à celles de l’alphabet usuel. On remarque bien un pic sur E puis deux petits pics au niveau de L-M-N-O-P et de R-S-T-U. Chaque lettre serait donc codée par la même lettre, ce qui signifie que la deuxième lettre du mot-clé serait A. Nous avons le début de notre mot-clé, que l’on peut écrire M-A-L3-L4-L5. En analysant de la même manière la 3e, la 8e, la 13e,… lettres nous découvrons que la 3e lettre du mot-clé est G. L’analyse de la quatrième lettre nous donne I, et la cinquième E. Le mot-clé est MAGIE.
- Il est maintenant possible d’utiliser le carré de Vigenère et de compléter la cryptanalyse. La première lettre cryptée est A et elle a été cryptée selon la première lettre du mot-clé M. En nous reportant au carré de Vigenère, nous cherchons la lettre A dans la ligne commençant par M et nous remontons jusqu’à la lettre en tête de cette colonne. Il s’agit de O, qui est donc la première lettre du texte clair.
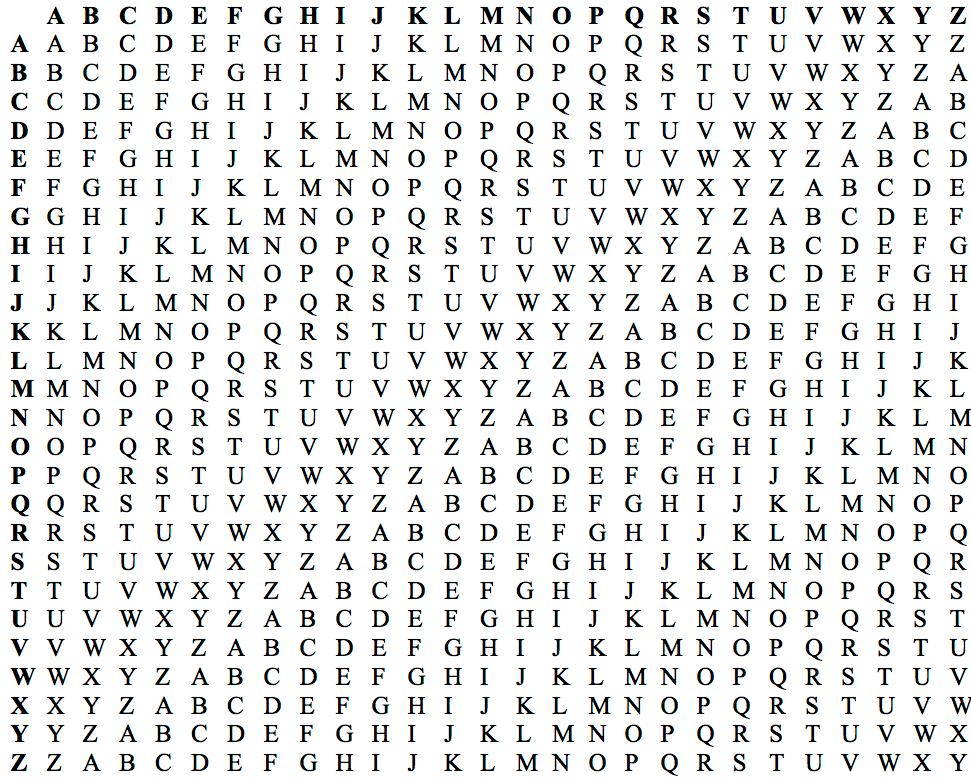
La table de Vigenère
- Nous obtenons ainsi le début du texte en clair : “OTEMPSSUSPENDSTONVOL…”. En séparant les mots les uns des autres et en insérant la ponctuation nécessaire, nous retrouvons le texte :
Ô temps ! suspends ton vol, et vous, heures propices !
Suspendez votre cours :
Laissez-nous savourer les rapides délices
Des plus beaux de nos jours !Assez de malheureux ici-bas vous implorent,
Coulez, coulez pour eux ;
Prenez avec leurs jours les soins qui les dévorent ;
Oubliez les heureux.Mais je demande en vain quelques moments encore,
Le temps m’échappe et fuit ;
Je dis à cette nuit : Sois plus lente ; et l’aurore
Va dissiper la nuit.
- Conclusion : ce sont les vers du poète Alphonse de Lamartine extraits du poème Le Lac, codés avec le chiffre de Vigenère.