La Cryptographie Quantique n’est pas à proprement parler une nouvelle forme de cryptographie dans le sens où elle n’offre pas de nouveau protocole de chiffrement. Elle offre en revanche un moyen extrêmement sécurisé de transmettre un message aléatoire et secret entre deux correspondants. On parle de distribution quantique des clefs.
Ce protocole de distribution quantique des clefs nécessite un canal de communication quantique, comme une fibre optique, où peuvent circuler des éléments quantiques polarisés, comme des photons.
Petit rappel sur la polarisation…
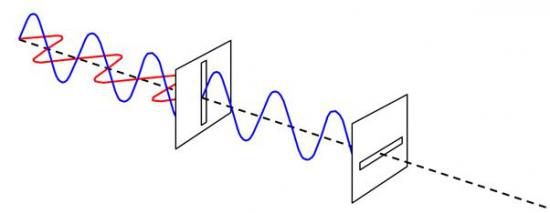
Schéma d'une onde lumineuse polarisée de manière rectiligne, passant par des filtres polarisants
Il existe plusieurs types de polarisation des ondes, rectiligne, circulaire ou elliptique. C’est la polarisation rectiligne qui nous intéresse. La lumière peut être polarisée de manière rectiligne selon tous les axes du plan d’onde par des filtres polarisants.
La seule chose à connaître est que les photons sont certains de passer un filtre polarisant si et seulement si ils sont polarisés dans la même direction. Un photon polarisé “verticalement” (90°) traversera un filtre polarisant “vertical” (90°), mais sera arrêté par un filtre polarisant “horizontal” (0°), car leurs polarisations sont perpendiculaires l’une à l’autre.
Des polarisations rectilignes ou diagonales
Dans le protocole que nous allons vous présenter, les photons pourrons prendre 4 polarisations différentes : 0°, 45°, 90° et 135°.
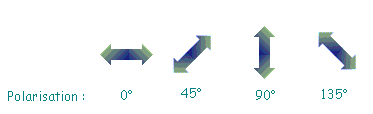
Les 4 polarisations différentes : 0°, 90°, 45° et 135°
Il est évident qu’un photon polarisé à 45° ne traversera pas un filtre polarisé à 135° puisque la polarisation du photon est perpendiculaire à celle du filtre. Mais qu’en est-il s’il essaye de traverser un filtre polarisé à 0° ou 90° ? La réponse est qu’il a exactement une chance sur deux.
Voici le tableau complet des 16 combinaisons possibles de photons et de filtres.
| Photon\Filtre | 0° | 90° | 45° | 135° |
|---|---|---|---|---|
| 0° | 1 | 0 | 0,5 | 0,5 |
| 90° | 0 | 1 | 0,5 | 0,5 |
| 45° | 0,5 | 0,5 | 1 | 0 |
| 135° | 0,5 | 0,5 | 0 | 1 |
Dans notre protocole nous utiliserons deux filtres seulement, un filtre dont la polarisation est rectiligne (0° ou 90°) et un laissant passer ceux dont la polarisation est diagonale (45° ou 135°).
| Photon\Filtre | 0° | 45° |
|---|---|---|
| 0° | 1 | 0,5 |
| 90° | 0 | 0,5 |
| 45° | 0,5 | 1 |
| 135° | 0,5 | 0 |
1 : le photon passe,
0 : il ne passe pas
0,5 : il a une chance sur deux
Mais à quoi cela nous sert-il ?
Dans la situation soumise à notre étude, il y a deux correspondants. Au hasard Alice veut envoyer des informations secrètes à Bob. Alice et Bob vont aussi avoir besoin d’un canal de transmission traditionnel, pas forcément sécurisé mais authentifié (Alice doit être absolument certaine qu’elle parle à Bob et vice-versa) où ils pourront discuter des modalités de la mise en place de l’échange quantique des clefs.
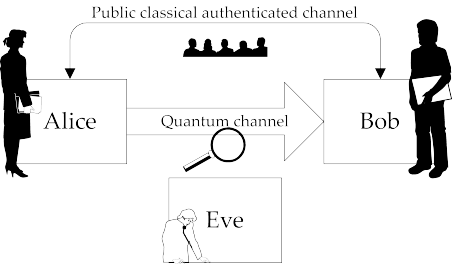
Schéma illustrant la situation étudiée
La clef qu’ils vont se transmettre va être composée de nombres binaires, des 0 et des 1. Ils vont se dire que les photons polarisés à 0° ou 45° représentent des 0 tandis que ceux polarisés à 90° ou 135° représentent des 1. Alice va envoyer sur le canal quantique des photons polarisés aléatoirement dans chacune des 4 polarisations proposées.
Connaître la polarisation d’un photon est impossible. La seule chose que Bob peut faire est de placer au hasard un de ses 2 filtres (rectiligne ou diagonal) et détecter si le photon est passé ou non. Si Bob a choisi le “bon” filtre, diagonal si c’était la polarisation initiale du photon ou rectiligne si cette dernière l’était, alors la mesure de Bob sera certaine et il connaitra la polarisation initiale du photon. Si Bob a choisi le “mauvais” filtre, alors il possède autant de chance d’obtenir un 0 ou un 1, aléatoirement et indépendamment de la polarisation initiale du photon.
On voit qu’une mesure de Bob sur deux est inutile, il faut donc les éliminer. C’est pour cela que Bob va envoyer a Alice quel filtre il a utilisé pour chaque photon, sur un canal clair. Et Alice va lui répondre pour chaque photon si Bob a utilisé le “bon” ou le “mauvais” filtre. Ils vont ensemble ignorer et oublier chacun des photons pour lesquels Bob a choisi le “mauvais” filtre.
Alice et Bob sont donc chacun en possession d’une série de nombres binaires identiques.
Pourquoi ce chiffrement est il sûr ?
Jusqu’à présent, le protocole que nous avons présenté permet juste de transmettre une série de nombres binaires de manière très lente, mais qu’est-ce qui empêche quelqu’un d’écouter le canal quantique pour connaître la polarisation de chacun des photons ? C’est un loi de la physique quantique, le principe d’incertitude d’Heisenberg. D’après Wikipédia :
Le principe d’incertitude de Heisenberg désigne toute inégalité mathématique affirmant qu’il existe une limite fondamentale à la précision avec laquelle il est possible de connaître simultanément deux propriétés physiques d’une même particule ; ces deux variables dites complémentaires peuvent être sa position et sa quantité de mouvement.
Autrement dit, il est prouvé de manière théorique que connaître la polarisation d’un photon est impossible. Un attaquant potentiel, ici Eve peut essayer de mesurer la polarisation d’un photon en placant un filtre au hasard et grâce à un capteur, voir si le photon est passé ou non. Ensuite, Eve doit renvoyer un photon, polarisé dans le même sens que celui qu’elle a reçu, mais comme Bob, Eve a une chance sur deux de choisir le “bon” filtre. Si elle a choisi le bon filtre, elle peut renvoyer le photon polarisé dans la même direction que celui qu’elle a reçu, et Alice et Bob ne s’apercevront de rien. Malheureusement pour Eve, si elle a choisi le “mauvais” filtre, alors elle ne pourra pas être certaine que le photon qu’elle va renvoyer sera polarisé dans le même sens que celui qu’elle a reçu. Il y a donc de fortes chances qu’elle se trompe et que Alice et Bob ne possèdent pas les mêmes nombres binaires secrets.
Pour vérifier qu’un attaquant n’écoute pas la ligne, Alice et Bob vont décider de communiquer publiquement une partie, certains bits choisis aléatoirement, de leur clef. Si certains bits sont différents, alors il est certain qu’un attaquant a espionné le canal quantique. Il est donc impératif que les correspondants oublient cette clef.
Plus Alice et Bob partagent de nombres binaires publiquement, plus ils seront certains que leur communication est sécurisée.