Eléments de contexte : la Grèce Antique
La scytale est le premier système de cryptographie connu. Il a été utilisé à des fins militaires lors des guerres médiques qui ont opposé la Perse et les cités autonomes de Grèce au Ve siècle avant J-C.
Ces dernières furent déclenchées par la révolte des cités grecques d’Ionie (littoral d’Asie Mineure) contre la domination perse. Les deux expéditions militaires des souverains perses Darius Ier et Xerxès Ier constituent les principaux épisodes militaires de ce conflit ; elles se conclurent par la victoire spectaculaire des cités grecques européennes conduites par Athènes et Sparte.
Des plans d’invasions sophistiqués y virent le jour et, pour la première fois, il apparaissait nécessaire d’établir un moyen de communication secret entre le front et l’arrière. La scytale fut alors inventée dans la cité de Sparte.
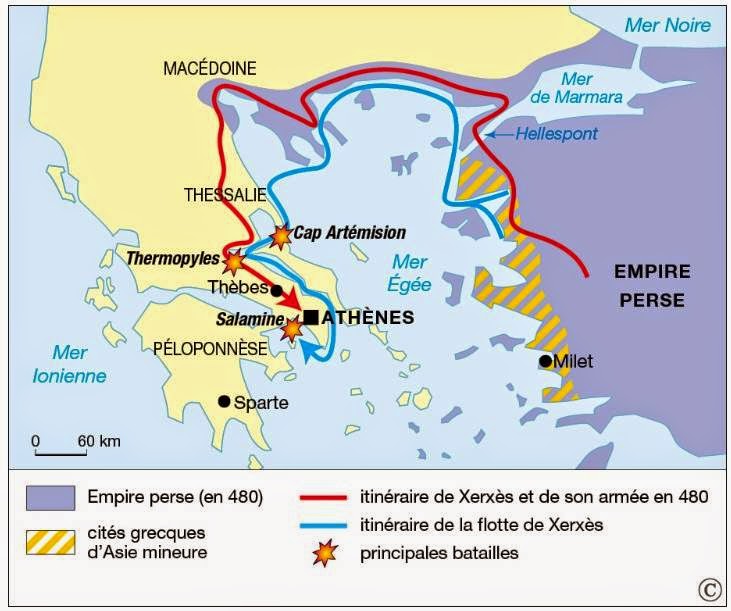
Carte légendée des guerres médiques
Le terme skutalê désigne dans sa première acception le gros bâton ou le fouet mais à Sparte, selon les descriptions qu’en donnent Victor Ehrenberg , J. Oelherdans et Albert Martin la skutalê a un sens et un emploi particuliers : le bâton servait à chiffrer et à déchiffrer des missives secrètes. Ce dispositif n’existait qu’à Sparte et seules les élites de la cité, les éphores (les magistrats du gouvernement) et les généraux, en connaissaient le procédé.
Fonctionnement de la scytale et modélisation mathématique

Plutarque, Ier siècle avant J.-C.
Plutarque, un écrivain majeur de la Rome antique venant de Grèce et ayant vécu au Ier siècle après J-C, rapporta le fonctionnement de la scytale dans Les Vies des Hommes Illustres :
« Voici, du reste, ce que c’est que la scytale. Quand un général part pour une expédition de terre ou de mer, les éphores prennent deux bâtons ronds, parfaitement égaux en longueur et en grosseur, de façon à se correspondre exactement l’un à l’autre, dans toutes les dimensions. Ils gardent l’un de ces bâtons, et donnent l’autre au général: ils appellent ces bâtons scytales. Lorsqu’ils veulent mander au général quelque secret d’importance, ils taillent une bande de parchemin, longue et étroite comme une courroie, la roulent autour de la scytale qu’ils ont gardée, sans laisser le moindre intervalle entre les bords de la bande, de telle sorte que le parchemin couvre entièrement la surface du bâton. Sur ce parchemin ainsi roulé autour de la scytale, ils écrivent ce qu’ils veulent ; et, quand ils ont écrit, ils enlèvent la bande, et l’envoient au général sans le bâton. Le général qui l’a reçue n’y saurait rien lire d’ailleurs, parce que les mots, tout dérangés et épars, ne forment aucune suite; mais il prend la scytale qu’il a emportée, et il roule alentour la bande de parchemin, dont les différents tours, se trouvant alors réunis, remettent les mots dans l’ordre dans lequel ils ont été écrits, et présentent toute la suite de la lettre. On appelle cette lettre scytale, du nom même du bâton, comme ce qui est mesuré prend le nom de ce qui lui sert de mesure. »
Tome 2 (traduction d’Alexis Pierron), Vie de Lysandre, p. 379.

Reconstitution d'une scytale avec 8 lettres par tour de ruban et une longueur de 8 lettres
Mathématiquement, on peut traduire cette technique de la manière suivante. On appelle T le nombre de lettres par tour de ruban (ce qui revient à connaître la taille du cylindre) et L le nombre de tours de ruban, c’est à dire la taille du message que l’on veut transmettre ou encore le nombre de lettres du message. Enfin, on nomme N le nombre total de lettres écrites sur le ruban. On peut ainsi dire que TxL = N. La personne en possession du ruban connaît forcément N (il lui suffit de compter le nombre de lettres inscrites), elle peut donc décoder le message si elle connaît T ou L.
Exemple
Imaginons que le texte à transmettre soit “Sparte” (6 lettres) et que la scytale ait un diamètre tel qu’on puisse y enrouler 3 lettres par tour. Le ruban déplié contiendra 6*3=18 lettres. Si un Perse intercepte le message et sait que ce dernier contient un mot de 6 lettres, il lui est facile de retrouver la taille de la scytale lui permettant de lire le message secret. En effet, si TxL=N alors T = N/L donc dans notre cas T = 18/6 = 3. Le Perse sait alors qu’il lui faut un cylindre permettant d’enrouler 3 lettres et peut lire le message en clair.
Faiblesse
Lorsque l’on sait que le texte a été chiffré avec la scytale, on peut essayer de lire une lettre sur deux, sur trois, sur quatre, jusqu’à ce que le texte prenne sens : cela revient à essayer tous les “T” possible. Il s’agit d’une attaque par force brute qu’il est fort aisé de réaliser.
A vous de jouer !
Le message ci-dessous est écrit sur un ruban à enrouler autour d’une scytale d’un diamètre tel qu’on lit 3 lettres par tour. Tentez de le déchiffrer. Petit indice : c’est une citation du philosophe grec Platon.
dteotvnurnraeesec!