Eléments de contexte
C’est en s’inspirant des travaux d’un bénédictin allemand, Johannes von Heidenberg, surnommé Trithème que Blaise de Vigenère élabora son fameux carré. En effet le moine avait eu l’idée “mettre en carré” les roues d’Alberti, ce qui aboutissait à un tableau de 26 lignes, la première étant composée d’un alphabet ordinaire, les autres d’un alphabet décalé à chaque fois d’un rang vers la gauche. Il chiffrait la première lettre du message avec la première ligne du tableau, la deuxième lettre avec la deuxième ligne et ainsi de suite jusqu’au moment où, parvenu à la dernière ligne du tableau, il repartait à la première. Le carré n’est pas alors exploité à son maximum : la notion de clef littérale émergea au début du XVIe siècle avec l’italien Belaso qui parlait de “mot de passe”. Vigenère fit la synthèse des deux en reprenant le tableau de Trithème et en l’utilisant avec le principe de clef de Belaso : il changea d’alphabet à chaque nouvelle lettre.

Blaise de Vigenère
Modélisation mathématique et fonctionnement
Les correspondants définissent préalablement une clef qui servira à chiffrer et déchiffrer leurs messages. Le mot-clef est épelé bien clairement au-dessus du message, et répété en boucle de sorte que chaque lettre du message soit associée à une lettre de la clef. Ils décalent ensuite la lettre du message du nombre associé à la lettre de la clef correspondante (A associé à 0, B à 1, etc…).
Exemple : Vigenère est remarquable avec comme clef : crypto
| Clair | V | I | G | E | N | E | R | E | E | S | T | R | E | M | A | R | Q | U | A | B | L | E |
| Clef | C | R | Y | P | T | O | C | R | Y | P | T | O | C | R | Y | P | T | O | C | R | Y | P |
| Chiffré | X | Z | E | T | G | S | T | V | C | H | M | F | G | D | Y | G | J | I | C | S | J | T |
Dans le tableau de Vigenère, les lignes sont pour la clef et les colonnes pour l’alphabet clair. La lettre chiffrée se trouve à l’intersection entre la ligne de la clef et la colonne de la lettre claire. Pour chiffrer la première lettre, V, on identifie la lettre de la clef placée au-dessous, C, qui détermine la ligne. On repère ensuite la colonne commençant par V et on repère la lettre se trouvant à l’intersection de la ligne C et de la colonne V, c’est bien X.
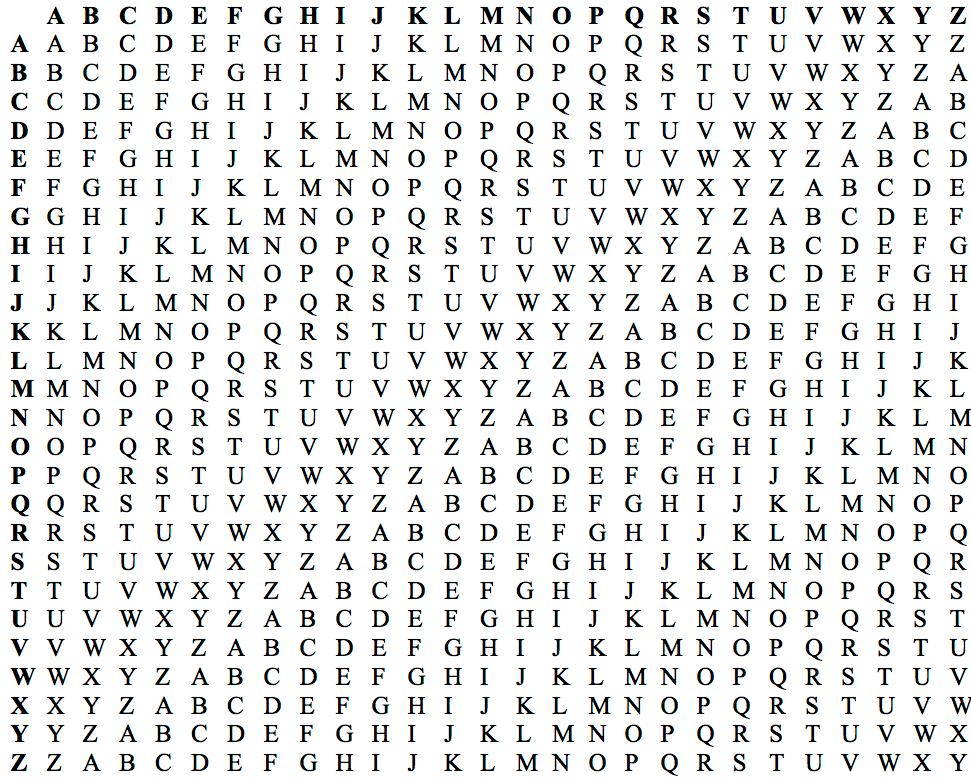
La table de Vigenère
Voici donc une modélisation mathématique par une fonction, qui, définie sur les entiers de 0 à 25 associe au nombre correspondant à la lettre claire, le nombre correspondant à la lettre chiffrée
\[f(l_{i}) = (l_{i} + k_{i} \bmod k) \bmod 26\]Où :
| $$ i $$ | position de la lettre chiffrée et claire dans le message |
| $$ l_{i} $$ | nombre associé à la lettre d’indice i |
| $$ k_{i} $$ | nombre associé à lettre de la clef d’indice i |
| $$ k $$ | taille de la clef |
Sécurité
Vigenère tire son savoir des cryptologues italiens qu’il a rencontrés lors de séjours diplomatiques à Rome : il expose sa théorie dans le Traité des chiffres ou secrètes manières d’écrire paru en 1585. C’est un chiffrement polyalphabétique qui résiste donc à l’analyse des fréquences des cryptanalystes arabes. Plus la clef est grande, plus le niveau de sécurité est élevé. Donc si la clef de chiffrement est aussi longue que le message, et totalement aléatoire, le chiffre de Vigenère est inviolable : on parle de méthode du masque jetable, de chiffrement de Vernam, ou de One-Time Pad. Celui-ci est notamment utilisé pour le téléphone rouge et encore aujourd’hui dans les ambassades. Cependant pour utiliser le chiffrement de Vernam il faut au préalable transmettre à son correspondant une clef aléatoire aussi longue que le message. On ne fait donc que déplacer le problème, mais dans des cas comme celui du téléphone rouge, on peut se permettre de transmettre la clef par des valises diplomatiques.
Pour chiffrer automatiquement :
A vous de jouer !
Le message suivant a été codé avec la clef RABELAIS. Tentez de le déchiffrer.
Jcjiycm krnt gznauzeogp n’mkk qvi cuqfv df p’lmm